圆形面积的计算方法（多种方法巧求与圆有关的阴影部分面积）

一、直接法（或公式法）

适用情形：阴影部分是一个规则的几何图形，例如三角形、矩形等；

解法：直接利用公式计算。

例1、如图，长方形的宽为4，M，N为两宽的中点，以底边BC的中点E为圆心，EN为半径画弧，正好与矩形上边相切于点F，求图中阴影部分的面积。

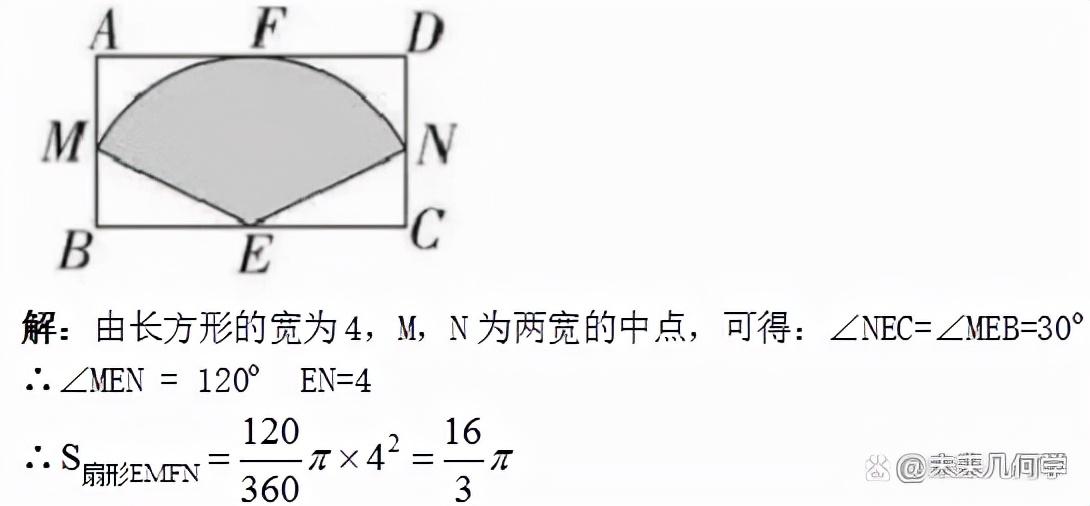
二、和差法

适用情形：与直接法相反，图中有一部分空白是一个规则的几何图形，而这部分空白与阴影部分的结合也是一个规则的几何图形或几个规则几何图形的组合。

解法：直接利用规则图形的和差求面积。

例2、如图，在边长为4的正方形ABCD中，先以点A为圆心，AD的长为半径画弧，再以AB边的中点为圆心，AB长的一半为半径画弧，则阴影部分面积是________(结果保留π)．

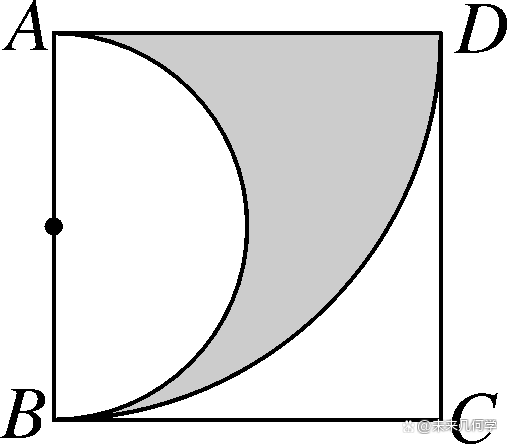
解：π×4²÷4-π×2²÷2=2π

例3、如图，长方形ABCD的长BC为3cm，宽AB为2cm，点E，F是边AD的三等分点，点G，H是边BC的三等分点．现分别以B，G两点为圆心，以2cm长为半径画弧AH和弧EC，则阴影部分的面积为________cm2.

三、　割补法

适用情形：适用于可将图中部分阴影通过对称分割，然后通过旋转和平移，补到另外一块阴影部分上去，构成一个规则的几何图形，如扇形，矩形，三角形等。

例4、如图，将半径为3的圆形纸片，按下列顺序折叠，若弧AB和弧BC都经过圆心O，则阴影部分的面积是（ ）

四、等积法

适用情形：①图中某些空白部分和阴影部分面积相等，可通对称、旋转，使之成为较为规则图形；②用同底等高的三角形等积替换

五、利用全等三角形

适用情形：图形较为复杂，普通方法不易求解，观察是否可以通过作辅助线，证明某两个三角形全等，然后再通过以上四种方法求解。